学生意識調査 2003
W2 相関と回帰菅野 剛
Abstract
Abstract
数式
1. クロス集計と散布図
1.1. クロス集計
tmp <- table(父親巨人好き = nu03$R14, 本人巨人好き = nu03$R13)
tmp
本人巨人好き
父親巨人好き 大嫌い やや嫌い やや好き 大好き
大嫌い 10 3 2 0
やや嫌い 2 21 13 1
やや好き 4 12 30 5
大好き 2 15 24 7
| 父親\本人 | 大嫌い | やや嫌い | やや好き | 大好き |
|---|---|---|---|---|
| 大嫌い | 10 | 3 | 2 | 0 |
| やや嫌い | 2 | 21 | 13 | 1 |
| やや好き | 4 | 12 | 30 | 5 |
| 大好き | 2 | 15 | 24 | 7 |
1.2. モザイクプロット
par(family = "HiraKakuProN-W3") ## ← Windowsでは実行しない mosaicplot(tmp, las = 1, main = "父親巨人好き と 本人巨人好き")
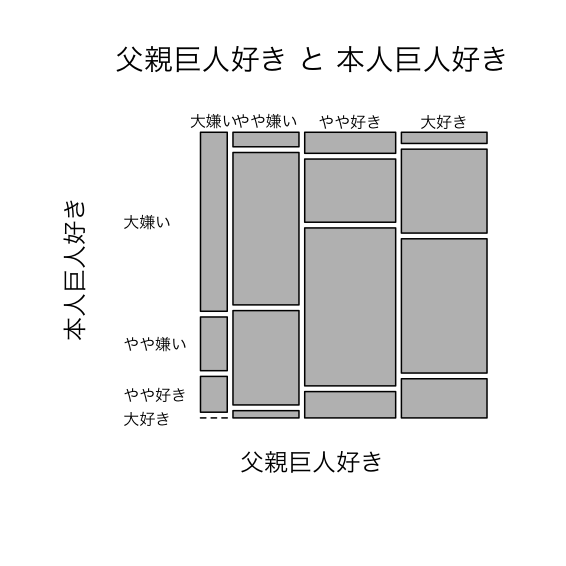
図1: モザイクプロット 父親巨人好き と 本人巨人好き
1.3. 3D 棒グラフ

図2: 父親巨人好き と 本人巨人好き
1.4. クロス集計 周辺度数
addmargins(tmp) # addmargins() で周辺度数を計算
本人巨人好き
父親巨人好き 大嫌い やや嫌い やや好き 大好き Sum
大嫌い 10 3 2 0 15
やや嫌い 2 21 13 1 37
やや好き 4 12 30 5 51
大好き 2 15 24 7 48
Sum 18 51 69 13 151
| 父親\本人 | 大嫌い | やや嫌い | やや好き | 大好き | 合計 Sum |
|---|---|---|---|---|---|
| 大嫌い | 10 | 3 | 2 | 0 | 15 |
| やや嫌い | 2 | 21 | 13 | 1 | 37 |
| やや好き | 4 | 12 | 30 | 5 | 51 |
| 大好き | 2 | 15 | 24 | 7 | 48 |
| 合計 Sum | 18 | 51 | 69 | 13 | 151 |
1.5. クロス集計 行%
prop.table(tmp, 1)
本人巨人好き
父親巨人好き 大嫌い やや嫌い やや好き 大好き
大嫌い 0.66666667 0.20000000 0.13333333 0.00000000
やや嫌い 0.05405405 0.56756757 0.35135135 0.02702703
やや好き 0.07843137 0.23529412 0.58823529 0.09803922
大好き 0.04166667 0.31250000 0.50000000 0.14583333
round(prop.table(tmp, 1), 2) # round() で小数点以下2桁に限定
本人巨人好き
父親巨人好き 大嫌い やや嫌い やや好き 大好き
大嫌い 0.67 0.20 0.13 0.00
やや嫌い 0.05 0.57 0.35 0.03
やや好き 0.08 0.24 0.59 0.10
大好き 0.04 0.31 0.50 0.15
1.6. 散布図
par(family = "HiraKakuProN-W3") ## ← Windowsでは実行しない plot(nu03$r14, nu03$r13, main = "散布図 父親巨人好きと本人巨人好き", xlab = "父親巨人好き", ylab = "本人巨人好き")
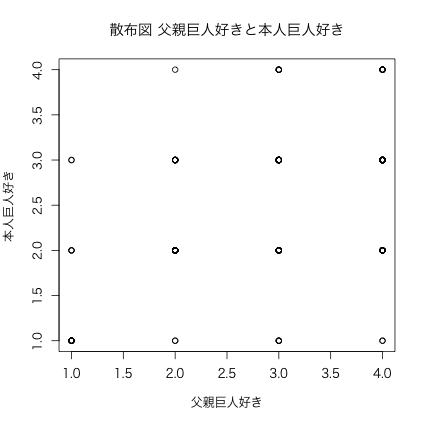
図3: 散布図 父親巨人好きと本人巨人好き
1.7. 散布図 jitter
par(family = "HiraKakuProN-W3") ## ← Windowsでは実行しない plot(jitter(nu03$r14), jitter(nu03$r13), main = "散布図 父親巨人好きと本人巨人好き (jitter)", xlab = "父親巨人好き", ylab = "本人巨人好き")
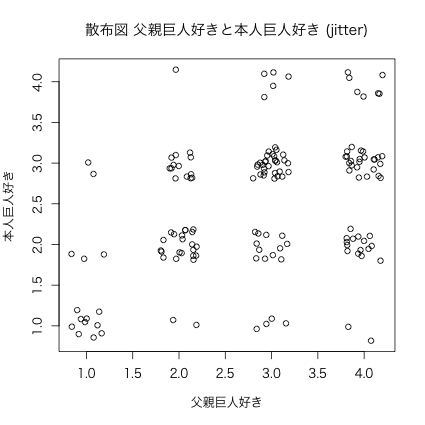
図4: 散布図 父親巨人好きと本人巨人好き
2. 相関係数
2.1. 相関係数 父親巨人好き vs 本人巨人好き
cor(nu03$r14, nu03$r13) # 欠測値 NA があると計算不可
[1] NA
cor(nu03$r14, nu03$r13, use = "pairwise") # ペアワイズ (ペアが揃っている) で計算
[1] 0.4082542
- ピアソンの積率相関係数 \(r_{xy} = \frac{s_{xy}}{s_x s_y} = 0.41\)
- 共分散 \(s_{xy} = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})\)
- 分散 \(s_x^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2\)
- 標準偏差 \(s_x = \sqrt{s_x^2}\)
- 分散 \(s_y^2 = \frac{1}{n-1} \sum_{i=1}^n (y_i - \bar{y})^2\)
- 標準偏差 \(s_y = \sqrt{s_y^2}\)
2.2. 相関係数 父親巨人好き vs 本人巨人好き
- ピアソンの積率相関係数 = 0.41

図5: 散布図 父親巨人好きと本人巨人好き
3. 回帰直線
3.1. 回帰直線
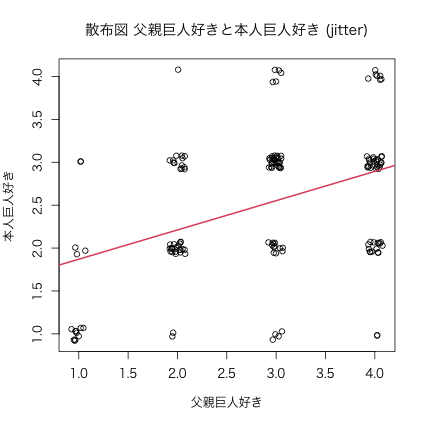
図6: 散布図 父親巨人好きと本人巨人好き
4. 回帰式
4.1. 回帰式
lm(r13 ~ r14, data = nu03)
Call:
lm(formula = r13 ~ r14, data = nu03)
Coefficients:
(Intercept) r14
1.5287 0.3414
formula = r13 ~ r14- 本人巨人好き = 切片 + 傾き * 父親巨人好き
- 切片 (Intercept) 1.5287
- 傾き 0.3414
- 本人巨人好き = 1.5287 + 0.3414 * 父親巨人好き
5. 回帰、決定係数
5.1. 回帰式 summary()
summary(lm(r13 ~ r14, data = nu03))
Call:
lm(formula = r13 ~ r14, data = nu03)
Residuals:
本人巨人好き
Min 1Q Median 3Q Max
-1.8943 -0.5529 0.1057 0.4471 1.7885
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.52865 0.18975 8.056 0.000000000000234 ***
r14 0.34141 0.06254 5.459 0.000000195495263 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7469 on 149 degrees of freedom
( 2 個の観測値が欠損のため削除されました )
Multiple R-squared: 0.1667, Adjusted R-squared: 0.1611
F-statistic: 29.8 on 1 and 149 DF, p-value: 0.0000001955
- 本人巨人好き = 1.52865 + 0.34141 * 父親巨人好き
5.2. 回帰式
| Coefficients | Estimate | Std. Error | t value | Pr(>|t|) |
|
|---|---|---|---|---|---|
| 係数 | 推定値 | 標準誤差 | t値 | 有意確率 | |
| (Intercept) | 1.52865 | 0.18975 | 8.056 | 0.000000000000234 | *** |
| 父親巨人好き | 0.34141 | 0.06254 | 5.459 | 0.000000195495263 | *** |
***0.1%有意 ,**1%有意 ,*5%有意 ,.10%有意 , 印なし 非有意- 本人巨人好き = 1.52865 + 0.34141 * 父親巨人好き
- 父親巨人好きは効果なし(帰無仮説)の元で、 0.341 という効果
- 0.341 を 標準誤差 0.06254 で割ると t値 5.459
- 自由度 150-1-1=149 で t値 5.459 が得られる確率は 0.000000195
- 帰無仮説 父親巨人好きは効果がない、を棄却
5.3. 回帰式
Residual standard error: 0.7469 on 149 degrees of freedom ( 2 個の観測値が欠損のため削除されました ) Multiple R-squared: 0.1667, Adjusted R-squared: 0.1611 F-statistic: 29.8 on 1 and 149 DF, p-value: 0.0000001955
- 残差の標準誤差 Residual standard error: 0.7469
- 自由度 149 degrees of freedom
- 決定係数 Multiple R-squared: 0.1667
- 修正決定係数 Adjusted R-squared: 0.1611
- F比 F-statistic: 29.8
- 自由度 1 and 149 DF
- p値 p-value: 0.0000001955
6. 相関と因果
6.1. 相関と因果
- 相関と因果は、異なる
- 回帰分析の説明変数と被説明変数の設定は、分析者に委ねられる
- 設定をすれば、回帰分析の結果は求まってしまう
- 全く見当違いの分析も、計算されてしまう
- 回帰分析の結果から、因果関係の向きを特定することは出来ない
- 過去の経験、知見、先行研究が重要
6.2. 相関と因果
lm(r13 ~ r14, data = nu03)
Call:
lm(formula = r13 ~ r14, data = nu03)
Coefficients:
(Intercept) r14
1.5287 0.3414
- 父親 → 子供
- 父親が巨人を好きだと、子供も巨人を好きになる
- 子供巨人好き = 1.5287 + 0.3414 * 父親巨人好き
lm(r14 ~ r13, data = nu03)
Call:
lm(formula = r14 ~ r13, data = nu03)
Coefficients:
(Intercept) r13
1.6489 0.4882
- 子供 → 父親
- 子供が巨人を好きだと、父親も巨人を好きになる
- 父親巨人好き = 1.6489 + 0.4882 * 子供巨人好き
7. 分割表
7.1. 分割表
- 分割表・クロス集計表 (contingency table / cross tabulation)
- R では
table()
- R では
- 独立性の検定 (test for independence)
- クラメールのV係数 (Cramér's V)
- \(V = \sqrt{\frac{\chi^2}{n \cdot \mathrm{min}(r-1,c-1)}}\)
8. 例
9. info
9.1. 相関係数
- 相関係数 cf. (correlation) \(r_{xy}=\frac{s_{xy}}{s_x s_y}\) , \(r_{xy}=\frac{1}{n-1} \sum z_x z_y\)
- R では
cor()
- R では
- 散布図 cf. (scatter plot)
- R では
plot()
- R では
- 平方和 (SS:sum of squares) \(SS=\sum_{i=1}^n (x_i-\bar{x})^2\)
- 共分散 (分母をnとした場合の共分散) (covariance) \(s_{xy}=\frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\)
- R では
cov()
- R では
- 偏相関係数 (partial correlational coefficient) \(r_{xy\cdot z} = \frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{1-r_{xz}^2} \sqrt{1-r_{yz}^2}}\)
- R では
ppcor::pcor()
- R では
9.2. 単回帰分析
- 単回帰分析 cf. cf. (regression analysis) \(y=a+bx+\epsilon\)
- R では
lm()
- R では
- 独立変数 (independent variable)
- 従属変数 (dependent variable)
- 回帰直線 cf. (regression line) \(\hat{y}=a+bx\)
- R では
abline(lm())
- R では
- 切片 (intercept) \(a=\bar{y}-b{\bar{x}}\)
- 傾き (slope) \(b=r \frac{s_y}{s_x}\)
- 決定係数 cf. (R squared) \(R^2\)
- R では
summary(lm())
- R では
- 最小2乗法 cf. (least squares method)
- 相関関係と因果関係 (correlation and causation)
10. 文献
| [1] | ポール G.ホーエル. 初等統計学 第4版. 培風館, 1981. |