学生意識調査 2003
W1 記述統計菅野 剛
Push [Space] or [->]
Abstract
Abstract
数式
1. ケース、変数、尺度水準
1.1. 変数 variables
- Q1. あなたの性別を教えてください。
- 男性
- 女性
- Q1 は「性別」を尋ねる質問
- Q1 は「性別」という 変数 variable
- 変数 :個人ごとに値が変わる
- 男性だったり、女性だったり
- 変数 :個人ごとに値が変わる
1.2. 変数 variables
- Q2. あなたの学年を教えてください。
- 1年
- 2年
- 3年
- 4年
- Q2 は「学年」を尋ねる質問
- Q2 は「学年」という 変数 variable
- 変数 :個人ごとに値が変わる
- 1年だったり、2年だったり
- 変数 :個人ごとに値が変わる
1.3. ケース cases
- 回答やデータの単位を ケース という
- 社会調査では、回答者一人一人が ケース
- ケース1:Aさんが、男性、2年と回答
- ケース2:Bさんが、男性、4年と回答
- ケース3:Cさんが、男性、2年と回答
1.4. ケース cases
- 野球チームの統計では、チームが ケース
- ケース1:巨人の優勝回数は…
- ケース2:阪神の優勝回数は…
- 都道府県別の統計では、県が ケース
- 国別の統計では、国が ケース
1.5. ケースと変数
| 変数 1 | 変数 2 | \(\cdots\) | |
|---|---|---|---|
| ケース 1 | 1 | 2 | \(\cdots\) |
| ケース 2 | 1 | 4 | \(\cdots\) |
| ケース 3 | 1 | 2 | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| ケース 153 | 1 | 3 | \(\cdots\) |
1.6. 変数とケース
| ケース 1 | ケース 2 | \(\cdots\) | |
|---|---|---|---|
| 変数 1 | 1 | 1 | \(\cdots\) |
| 変数 2 | 2 | 4 | \(\cdots\) |
| 変数 3 | \(\vdots\) | \(\vdots\) | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
- 行と列が入れ替わって表示される場合もある
- 見栄えが違うだけで、データは同じ
1.7. 尺度水準 levels of measuremnt
- 変数 の 尺度水準 によって、分析法が変わるので、重要
- カテゴリカル変数 categorical variables
- 量的変数 quantitative variables
- 違いの区分、順序がある、加減ができる、乗除ができる
- 社会調査では、 名義尺度 と 順序尺度 の変数が多い
- 順序尺度を間隔尺度とみなしての分析も多い
1.8. 量的変数の種類
- 量的変数 quantitative variables
- 離散変数 (discrete variable)
- 整数の値をとる
- 連続変数 (continuous variable)
- 小数の値もとる
- 離散変数 (discrete variable)
1.9. 名義尺度 nominal
- 違いの区分のみの情報をもつ
- 順番に意味がない
- 代表値 は、 最頻値
- Q1. あなたの性別を教えてください。
- 男性 ←
- 女性
- Q1. あなたの性別を教えてください。
- 女性
- 男性 ←
- 男女に割り振る数値が逆でも、意味は変わらない
- 数値は、区分の違いのためだけに使われる
- 1.男性 + 2.女性 = 3. ?? という計算は無理
- 関西、関東といった地域区分など
1.10. 順序尺度 ordinal
- 順序 に意味がある
- 順序 を変えると、情報がおかしくなる
- 代表値 は、 中央値
- Q2. あなたの学年を教えてください。
- 1年
- 2年
- 3年
- 4年
- 順序 に加え、計算ができると 間隔尺度
- ただし、大学1年 + 大学3年 = 大学4年 とはならない
- 年月は計算できるが、学年は、間隔尺度ではない
- 社会調査では、順序尺度を間隔尺度とみなす分析も多い
1.11. 間隔尺度 interval
- 順序 に加え、足し算・引き算ができると 間隔尺度
- 代表値 は、 算術平均
- よく紹介される例として、摂氏(C)や華氏(F)の温度
- 冬、10度
- 春、20度は、10度より10度高くなった
- 夏、30度は、20度より10度高くなった
- 0に意味があり、かけ算割り算ができると 比率尺度
- 温度 0度は人間が恣意的に割り振ったもの
- 10度の2倍が20度、という計算はできない
1.12. 比率尺度 ratio
- 0 に意味があり、かけ算割り算ができると 比率尺度
- 代表値 は、 算術平均 、 幾何平均 、 調和平均
- 絶対温度(K) は、絶対0度(熱振動停止)に意味がある
- 長さ、重さ、密度、時間、年齢、年収、来場者数
- Q16. 睡眠について伺います。あなたは大体どのくらい寝ますか?
- 1日に平均____時間
- Q24. 趣味や好きなことのために自由に使える、一ヶ月あたりのお金の金額はどのくらいですか?
- _______円ぐらい
2. データ・マトリクスと度数分布
2.1. データ・マトリクス data matrix
| gender | grade | \(\cdots\) | |
|---|---|---|---|
| 1 | 1 | 2 | \(\cdots\) |
| 2 | 1 | 4 | \(\cdots\) |
| 3 | 1 | 2 | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 153 | 1 | 3 | \(\cdots\) |
- 153人が 111 変数 に回答、 153×111=16983 もの数字
- 回答者の ケース 1〜153 が、1行ずつ積み重なっている
- 変数 が、q01 から順に1列ずつ 111 変数 分並んでいる
- 膨大な数字を見ても意味不明
- 変数 ごとに 代表値 や ばらつき を計算し特徴を把握
2.2. データのラベル化
| 性別 | 学年 | \(\cdots\) | |
|---|---|---|---|
| 1 | 男性 | 2年 | \(\cdots\) |
| 2 | 男性 | 4年 | \(\cdots\) |
| 3 | 男性 | 2年 | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 153 | 男性 | 3年 | \(\cdots\) |
- 153人の ケース が 111 変数 に回答
- ケース ごとに、 変数 の値が並ぶ
- ケース 1の回答者は、性別は男性で、学年は2年で …
- ケース 2の回答者は、性別は男性で、学年は4年で …
- ケース 3の回答者は、性別は男性で、学年は2年で …
3. グラフ、分布の形
3.1. 名義尺度 Gender 性別
- nu03 データの Gender 性別
table(n03$Gender) prop.table(table(n03$Gender))
男性 女性
91 62
男性 女性
0.5947712 0.4052288
addmargins(table(n03$Gender)) addmargins(prop.table(table(n03$Gender)))
男性 女性 Sum
91 62 153
男性 女性 Sum
0.5947712 0.4052288 1.0000000
3.2. 名義尺度 Gender 性別
pie(table(n03$Gender))
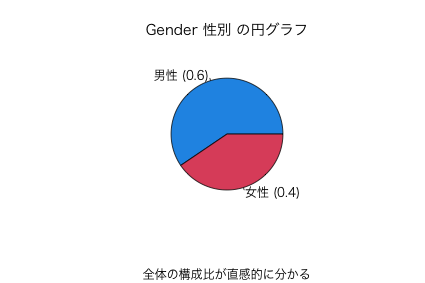
図1: Gender 性別 の円グラフ
3.3. 名義尺度 Gender 性別
barplot(table(n03$Gender)
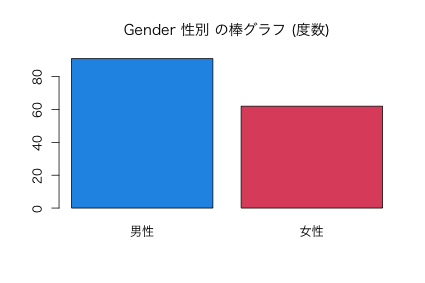
図2: Gender 性別 の棒グラフ (度数)
3.4. 名義尺度 Gender 性別
barplot(prop.table(table(n03$Gender))
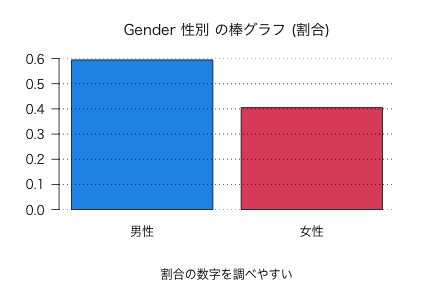
図3: Gender 性別 の棒グラフ (割合)
3.5. 名義尺度 Gender 性別
Hmisc::describe(n03$Gender)
n03$Gender : 性別
n missing distinct
153 0 2
Value 男性 女性
Frequency 91 62
Proportion 0.595 0.405
3.6. 順序尺度 Q06 通学時間
- Q06. 通学時間(片道)はどのくらいですか?
- 30分未満
- 30分〜1時間未満
- 1時間〜1時間半未満
- 1時間半〜2時間未満
- 2時間以上
table(n03$q06)
1 2 3 4 5 29 38 42 31 13
3.7. 順序尺度 Q07a 本を読む
- Q07. あなたは、以下の過ごし方をどの程度しますか?
a. 本を読む
- ほぼ毎日
- 最低一週1回
- 最低一月1回
- たまにする
- しない
head(subset(n03, , c(Gender, Grade, Q07a)))
Gender Grade Q07a 1 男性 2年 たまにする 2 男性 4年 ほぼ毎日 3 男性 2年 最低月1回 4 男性 2年 最低週1回 5 女性 2年 ほぼ毎日 6 女性 2年 最低週1回
3.8. r07a の作成
- 数値
q07aから 因子Q07aを作成
n03$r07a <- NULL n03$r07a <- 6 - n03$q07a label(n03$r07a) <- "生活:本を読む" describe(n03$r07a)
n03$r07a : 生活:本を読む
n missing distinct Info Mean Gmd
152 1 5 0.932 3.158 1.59
lowest : 1 2 3 4 5, highest: 1 2 3 4 5
Value 1 2 3 4 5
Frequency 17 52 13 30 40
Proportion 0.112 0.342 0.086 0.197 0.263
3.9. 因子 Q07a の作成
n03$Q07a <- NULL n03$Q07a <- ordered( factor(n03$q07a, levels = 1:5, labels = c("ほぼ毎日", "最低週1回", "最低月1回", "たまにする", "しない"))) label(n03$Q07a) <- "生活:本を読む" table(n03$Q07a)
ほぼ毎日 最低週1回 最低月1回 たまにする しない
40 30 13 52 17
3.10. 因子 Q07a の確認
head(n03$Q07a) # head() で最初の 6 オブザベーションを表示
生活:本を読む [1] たまにする ほぼ毎日 最低月1回 最低週1回 ほぼ毎日 最低週1回 Levels: ほぼ毎日 < 最低週1回 < 最低月1回 < たまにする < しない
table(n03$Q07a)
ほぼ毎日 最低週1回 最低月1回 たまにする しない
40 30 13 52 17
round(prop.table(table(n03$Q07a)), 2) # 割合を計算
ほぼ毎日 最低週1回 最低月1回 たまにする しない
0.26 0.20 0.09 0.34 0.11
3.11. 因子 R07a の作成
n03$R07a <- NULL n03$R07a <- ordered( factor(n03$r07a, levels = 1:5, labels = c("しない", "たまにする", "最低月1回", "最低週1回", "ほぼ毎日"))) label(n03$R07a) <- "生活:本を読む" head(n03$R07a)
生活:本を読む [1] たまにする ほぼ毎日 最低月1回 最低週1回 ほぼ毎日 最低週1回 Levels: しない < たまにする < 最低月1回 < 最低週1回 < ほぼ毎日
3.12. Q07a 本を読む 円グラフ
pie(table(n03$Q07a))
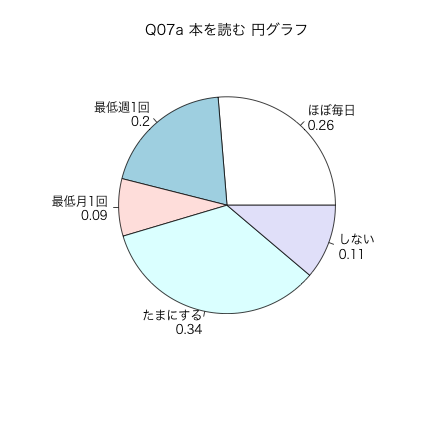
図4: Q07a 本を読む 円グラフ
3.13. Q07a 本を読む 棒グラフ
barplot(table(n03$Q07a))
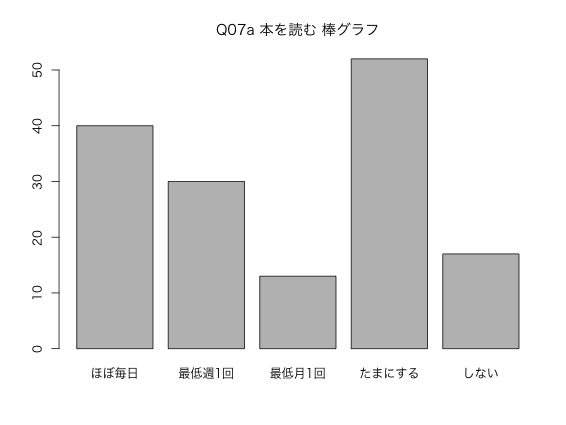
図5: Q07a 本を読む 棒グラフ
3.14. 比率尺度 q16 睡眠時間
| Gender 性別 | q16 睡眠時間 | \(\cdots\) | |
|---|---|---|---|
| 1 | 男性 | \(\cdots\) | |
| 2 | 男性 | 8 | \(\cdots\) |
| 3 | 男性 | 4 | \(\cdots\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 153 | 男性 | 5 | \(\cdots\) |
3.15. 比率尺度 q16 睡眠時間
summary(n03$q16)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 1.000 6.000 6.000 6.257 7.000 10.000 1
| 統計量 | 英語 | 値 |
|---|---|---|
| 最小値 | Minimum | 1 |
| 第1四分位数 | 1st Quantile | 6.000 |
| 中央値 | Median | 6.000 |
| (算術)平均 | Mean | 6.257 |
| 第3四分位数 | 3rd Quantile | 7.000 |
| 最大値 | Maximum | 10.000 |
| 欠測値 | NA's | 1 |
3.16. 比率尺度 q16 睡眠時間
Hmisc::describe(n03$q16)
n03$q16 : 睡眠時間
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75
152 1 10 0.906 6.257 1.293 4.55 5.00 6.00 6.00 7.00
.90 .95
8.00 8.00
lowest : 1 2 3 4 5, highest: 6 7 8 9 10
Value 1 2 3 4 5 6 7 8 9 10
Frequency 1 1 2 4 22 64 38 16 2 2
Proportion 0.007 0.007 0.013 0.026 0.145 0.421 0.250 0.105 0.013 0.013
3.17. 比率尺度 q16 睡眠時間
hist(n03$q16)
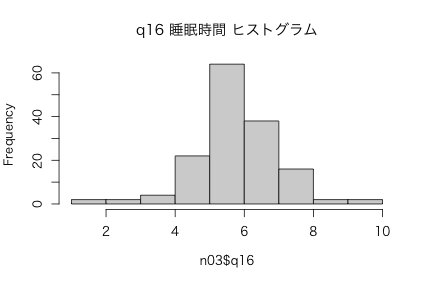
図6: q16 睡眠時間 ヒストグラム
3.18. 比率尺度 q16 睡眠時間
boxplot(n03$q16)
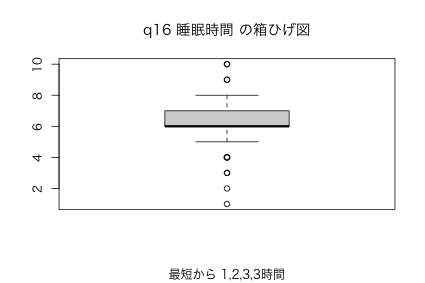
図7: q16 睡眠時間 の箱ひげ図
3.19. 議論
- q16 あなたは大体どのくらい寝ますか? 1日に平均____時間
- 睡眠時間 で 1,2,3,3,4,4,4,4時間という回答
- 実際に 1〜3時間かもしれない
- 記入ミスや不正確な回答かもしれない
- 外れ値として除外するか慎重に検討
- 睡眠時間 で 1,2,3,3,4,4,4,4時間という回答
4. 最頻値、中央値、平均
4.1. 最頻値 mode
n03$Gender # データ名$変数名 として値を全て出力
性別 [1] 男性 男性 男性 男性 女性 女性 女性 男性 男性 男性 男性 男性 女性 男性 女性 女性 男性 男性 男性 [20] 男性 男性 女性 女性 男性 男性 男性 男性 男性 男性 男性 男性 男性 男性 男性 女性 男性 男性 男性 [39] 男性 女性 女性 女性 男性 女性 女性 男性 男性 男性 女性 女性 男性 男性 女性 女性 女性 女性 男性 [58] 女性 女性 女性 女性 男性 女性 女性 女性 男性 男性 女性 女性 男性 女性 女性 男性 女性 女性 男性 [77] 男性 男性 男性 女性 女性 男性 男性 男性 女性 男性 女性 男性 女性 女性 女性 女性 男性 男性 女性 [96] 男性 男性 男性 女性 男性 男性 男性 男性 女性 男性 男性 女性 女性 女性 女性 男性 男性 男性 女性 [115] 男性 男性 女性 男性 男性 女性 男性 男性 女性 男性 男性 女性 女性 男性 女性 男性 男性 男性 男性 [134] 男性 男性 男性 女性 男性 男性 女性 男性 男性 女性 女性 男性 男性 女性 女性 男性 男性 女性 男性 [153] 男性 Levels: 男性 女性
table(n03$Gender) # table() 関数で度数分布を作成
男性 女性 91 62
- この場合、 最頻値 は「男性」
4.2. 中央値 median
label(n03$q21a) summary(n03$q21a)
[1] "ストレス:頻度" Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 2.366 3.000 5.000
- 中央値 Median は 2
4.3. 平均 mean
- 総和記号 (シグマ) (summation) \(\sum\)
- R では
sum()
- R では
- 平均 (エックス・バー) (mean) \(\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\)
- R では
mean()
- R では
head(n03$q16) # head() 最初の 6 オブザーべションを表示
睡眠時間 [1] NA 8 4 6 6 6
mean(n03$q16) # 欠測値 (NA) が含まれていると、計算不可
[1] NA
mean(n03$q16, na.rm = TRUE) # 欠測値 (NA) を除外 (ReMove) して、平均を計算
[1] 6.256579
- 平均睡眠時間は 6.25時間、6時間15分ほど
4.4. 外れ値
- 箱ひげ図で、四分位範囲の 1.5 倍以上離れている 外れ値 を確認
head(sort(n03$q16), 20)
睡眠時間 [1] 1 2 3 3 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5
4.5. 外れ値を探る
boxplot.stats(sort(n03$q16))
$stats 睡眠時間 [1] 5 6 6 7 8 $n [1] 152 $conf [1] 5.871845 6.128155 $out 睡眠時間 [1] 1 2 3 3 4 4 4 4 9 9 10 10
4.6. 外れ値の除外
- 3時間以上を対象とした場合の平均睡眠時間
summary(subset(n03, n03$q16 >= 3, q16))
q16
Min. : 3.00
1st Qu.: 6.00
Median : 6.00
Mean : 6.32
3rd Qu.: 7.00
Max. :10.00
- 平均は 6.32 時間あたり
4.7. 刈り込み平均 trim
mean(n03$q16, trim = 0.1, na.rm = TRUE) # 欠測値を除外して計算
[1] 6.270492
- 6.27 時間 = 6時間 15分
5. 範囲(レンジ)、四分位範囲
5.1. 範囲(レンジ) range
- 範囲・レンジ (range)
- ばらつきとして、 最大値 と 最小値 の幅
- 2つの数値だけから求まるので、計算が楽
- 裏返せば、豊富なデータから2つの情報しか使っていない
- R では
range()でmin()とmax()が表示される
range(n03$q16, na.rm = TRUE) # 欠測値を除外して計算
[1] 1 10
5.2. 四分位範囲 IQR
- 四分位数 (quartile points)
- データを小さい値から大きな値へ並び替え
- データを4等分すると、3つの区切りができる
- 第1四分位数
- 第2四分位数 = 中央値
- 第3四分位数
- 四分位範囲 (IQR:interquartile range)
- ばらつきとして、 第3四分位数 - 第1四分位数 の幅
- R では
IQR()
summary(n03$q16) IQR(n03$q16, na.rm = TRUE) # 欠測値を除外して計算
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 1.000 6.000 6.000 6.257 7.000 10.000 1 [1] 1
5.3. 箱ひげ図 boxplot
- 箱ひげ図・ボックスプロット cf. (boxplot)
- 四分位数 、 最大値 、 最小値 、 外れ値 をプロット
- 第1四分位数 と 第3四分位数 で、箱を描く
- ヒストグラム に比べ、分布の特徴を把握しやすい
- R では
boxplot()

図8: q16 睡眠時間 の箱ひげ図
6. 分散、標準偏差
6.1. 分散 variance
- データのすべての情報を考慮して、ばらつきを捉える
- 平均を中心として、個々のデータがばらついている度合い
- 不偏分散 (注: 除数がnの分散 とは別) (unbiased variance) \(s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\)
- R では
var()
var(n03$q16, na.rm = TRUE) # 欠測値を除外して計算
[1] 1.582738
6.2. 標準偏差 standard deviation
- 分散は、二乗した数値 (単位が面積) のため、ばらつきの大小がわかりにくい
- 分散の正の平方根をとる (単位が長さ) と、解釈しやすい数値に戻る
- 標準偏差 (注: 除数がnの標準偏差 とは別) (standard deviation) \(s=\sqrt{s^2}\)
- R では
sd() - 標準偏差 = 1.26
- もし q16 睡眠時間が正規分布に従っている場合、
- 平均 6.3 ± 1 * 1.26 時間の範囲に約68%の人が該当
- 平均 6.3 ± 2 * 1.26 時間の範囲に約95%の人が該当
sd(n03$q16, na.rm = TRUE) # 欠測値を除外して計算
[1] 1.258069
7. Zスコア、標準化得点
7.1. Zスコア、標準化得点 Z-score
- 標準化 (standardization)
- 標準正規分布表で Z値をチェックすると、その範囲の起こりやすさが分かる
- Z値, Zスコア, 標準化得点 (Z-score) \(z=\frac{x-\bar{x}}{s}\)
- R では
scale()
head(n03$q16) # 最初の 6オブザベーションの睡眠時間
睡眠時間 [1] NA 8 4 6 6 6
head(scale(n03$q16)) # 最初の 6オブザベーションの睡眠時間の Zスコア
[,1]
[1,] NA
[2,] 1.3857912
[3,] -1.7936844
[4,] -0.2039466
[5,] -0.2039466
[6,] -0.2039466
8. info
8.1. 目的
8.2. 中学・高校の関連教材
- 以降、用語のリンク先は 主に中学・高校の関連教材 です(総務省、掲載終了の場合は国立国会図書館「インターネット資料収集保存事業(Web Archiving Project)」)。
8.3. 到達目標
- 到達目標 統計学で学ぶ概要をイメージできる。統計学を学ぶ準備ができる。学びを積み重ねることができる。学びを習慣化できる。
8.4. 第1回 概要
8.5. 第2,3回 記述統計
8.6. 第4,5回 相関と回帰
8.7. 第6,7回 確率
- 第6,7回 確率
- ものごとの起こりやすさを数値で表し、推測統計学に向けて準備をします。
8.8. 第8,9回 確率分布
8.9. 第10,11回 標本分布
8.10. 第12,13回 推定
8.11. 第14,15回 仮説の検定
8.12. R や Python について
- The R Project for Statistical Computing
- R言語
- Google Colaboratory で R を使う
- 参考 環境構築、ライブラリの紹介、参考文献・推薦図書・データセット(pdf) (R と Python の環境構築)
- 第7章 プログラミングの基本(pdf) (R と Python)
8.13. 用語 統計学
8.14. 用語 探索的データ解析 (EDA: Exploratory Data Analysis)
- 度数分布表 cf. (frequency table)
table() - 最頻値・モード cf. (Mode)
- ヒストグラム cf. (histogram)
hist() - 歪度 (わいど) (skewness)
e1071::skewness() - 尖度 (せんど) (kurtosis)
e1071::kurtosis() - 箱ひげ図・ボックスプロット cf. (boxplot)
boxplot() - 中央値・メディアン cf. (Median)
median() - 四分位数 (quartile points)
- 四分位範囲 (IQR:interquartile range)
IQR() - 範囲・レンジ (range)
range()min()max() - 要約統計量 (summary statistics)
summary() - 総和記号 (シグマ) (summation) \(\sum\)
sum() - 平均 (エックス・バー) (mean) \(\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i\)
mean() - 不偏分散 (注: 除数がnの分散 とは別) (unbiased variance) \(s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\)
var() - 標準偏差 (注: 除数がnの標準偏差 とは別) (standard deviation) \(s=\sqrt{s^2}\)
sd()
9. 文献
| [1] | ポール G.ホーエル. 初等統計学 第4版. 培風館, 1981. |